2021. 4. 10. 02:08ㆍNeural Networks/Time Series
Transformer를 사용한 Time Series Forecasting 모델입니다.
Transformer는 Attention을 사용하여 Sequence data를 처리하는 모델이며 자연어에서 큰 성과를 보였고 다양한 방면으로 뻗어나가는 모델입니다.
저자는 Transformer의 구조를 유지하며, $y_t$~$y_{t+n}$를 예측하기 위해 $y_{t-k}$~$y_{t-1}$의 시계열을 사용하는 구조를 제안합니다.
또한 몇가지 개선사항을 논문을 통해 제시했습니다.
내용은 어려운 부분들이 없으며, Transformer에 대해 궁금하신 분들은 다른 블로그를 먼저 참고해주세요.
논문에 대한 오역, 의역등이 다수 포함되어 있습니다.
댓글로 많은 의견 부탁드립니다.
Author : Haoyi Zhou, Shanghang Zhang, Jieqi Peng, Shuai Zhang, Jianxin Li, Hui Xiong, Wancai Zhang
AAAI2021 Best paper
Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting
Many real-world applications require the prediction of long sequence time-series, such as electricity consumption planning. Long sequence time-series forecasting (LSTF) demands a high prediction capacity of the model, which is the ability to capture precis
arxiv.org
1. Introduction
저자는 Long sequence time-series forecasting (LSTF) 문제를 해결하는데 관심이 있으며, LSTM은 이 문제를 해결하는데 주요 방법으로 사용되어왔다고 말합니다. 실제로 아래 그림과 같이 입력을 되먹임하는 구조의 LSTM은 좋은 성능을 보였습니다.

그런데 저자는 예측하고자 하는 시계열의 길이가 길어질수록 두 가지 문제가 발생하는 것을 확인했습니다.

시계열의 길이가 길어질수록, inference time (예측 시간)이 늘어나고, 정확도라고 할 수 있는 Mean Squared Error가 증가하는 것을 제시합니다. 그래서 Transformer를 적용하여 LSTF를 시도하고자 하는데 Tansformer에도 3가지 문제가 있다고 언급합니다.
- Transformer의 self-attention layer는 $\mathcal{O}(L^2)$의 연산을 수행해야 합니다.
- Self-attention을 쌓은 $J$개의 stacking layer는 $\mathcal{O}(J \cdot L^2)$의 메모리를 사용합니다.
- Transformer의 decoder는 LSTM과 같은 추론시간을 소모합니다.
저자는 위 문제를 보완한 Transformer를 위해 self-attention 연산 방법을 변경합니다. 그리고 생성모델과 비슷한 decoder를 통해 LSTF를 수행하고자 합니다.
2. Methodology
Transformer의 self-attention은 attention score로 다음과 같은 식을 계산합니다. 여기서 Softmax는 키와 쿼리의 관계성을 스케일링하는 역할을 합니다. 아래 식은 시그마 안에 시그마가 존재하기 때문에 길이 $L$의 제곱만큼 내적을 수행해야 함을 알 수 있습니다.
$$ \mathcal{A} \left( \mathbf{Q}, \mathbf{K}, \mathbf{V} \right) = \mathrm{Softmax} \left( \frac{\mathbf{Q} \mathbf{K}^T}{\sqrt{d}} \right) \mathbf{V} $$
위 식으로부터 Tsai et al. 2019가 제안하는 kernel smoother를 적용하면 $i$번째 쿼리 $q_i$의 attention score는 다음과 같이 쓸 수 있습니다.
$$ \mathcal{A} \left( \mathbf{q}_i, \mathbf{K}, \mathbf{V} \right) = \sum_{j} \frac{ k(\mathbf{q}_i,\mathbf{k}_j) }{\sum_{l} k(\mathbf{q}_i, \mathbf{k}_l)} \mathbf{v}_j = \mathbb{E}_{p \left( \mathbf{k}_j \mid \mathbf{q}_i \right)}\left[\mathbf{v}_j \right]$$
$$ p \left( \mathbf{k}_j \mid \mathbf{q}_i \right) = k \left( \mathbf{q}_i,\mathbf{k}_j \right) / \sum_{l} k\left(\mathbf{q}_i,\mathbf{k}_l\right), k\left(\mathbf{q}_i,\mathbf{k}_j\right) = \exp\left(\mathbf{q}_i\mathbf{k}_j^T / \sqrt{d}\right)$$
잠시 건너뛰어 논문의 appendix c에는 기존의 attention score 분포를 시각화하여 heatmap으로 표현했습니다.

그림을 통해 극히 일부 값들만 큰 attention score를 갖으며, 나머지 값들은 0 근처의 값을 갖는 것을 확인할 수 있습니다. 만약 softmax로 계산된 것과 비슷한 효과를 누릴 수 있는 함수가 있다면 어떨까요? 심지어 연산량이 softmax보다 적다면 self-attention의 softmax함수를 대체할 수 있을 것입니다. Kullback-Leibler divergence $D_{KL}$는 두 확률 분포의 차를 0보다 큰 범위로 수치화할 수 있는 훌륭한 distance measure입니다. 또한 이 measure는 두 확률 분포가 클수록 값이 커지는 특성을 갖고 있으며 엔트로피로 설명할 수 있습니다. 임의의 두 확률 분포 $p$와 $q$의 차이는 $D_{KL}\left(p \parallel q\right) = \sum p \log \frac{p}{q} = \sum p \log p - \sum p \log q$로 계산할 수 있습니다.
이제 softmax를 대체하는 다른 score를 계산해보려 합니다. 균일 분포는 길이가 $L$인 모든 부분에 대해 $1 / L$의 확률을 갖는 반면, 새로운 attention score는 0 근처에 굉장히 큰 밀도를 갖는 확률분포를 형성합니다. 새로운 attention score와 균일 분포의 $D_{KL}$을 계산한다면 softmax와 비슷한 의미를 갖는 새로운 score를 계산할 수 있게됩니다. 새로운 attention score는 연산단계에서 꽤 큰 이점을 갖습니다. 균일분포 $q$와 kernel smoother attention score $p$에 대한 $D_{KL}\left(q \parallel p\right)$를 계산하면 아래와 같으며, 실제로 해보시더라도 간단히 변형시키실 수 있습니다. 새로운 attention score $M$을 저자는 Log-Sum-Exp (LSE)라고 부르며, $D_{KL}$에서 상수항을 제외한 식이고 아래 두번째 식 입니다.
$$D_{KL}\left(q \parallel p\right) = \ln \sum_{l=1}^{L_K} e^{\mathbf{q}_i\mathbf{k}_l^T / \sqrt{d}} - \frac{1}{L_K} \sum_{j=1}^{L_K} \mathbf{q}_i\mathbf{k}_j^T / \sqrt{d} - \ln L_K$$
$$M\left(\mathbf{q}_i,\mathbf{K}\right) = \ln \sum_{l=1}^{L_K} e^{\mathbf{q}_i\mathbf{k}_l^T / \sqrt{d}} - \frac{1}{L_K} \sum_{j=1}^{L_K} \mathbf{q}_i\mathbf{k}_j^T / \sqrt{d}$$
그런데 새로운 self-attention 또한 특정 몇몇 쿼리 $\mathbf{q}_i$에 큰 가중치를 받습니다. 나머지 쿼리는 0 근처이며 해당 쿼리들이 다음 attention layer의 영향력이 항상 크다고는 말할 수 없습니다. 큰 가중치를 갖는 상위 쿼리 $u$개를 선택했을때 다음 layer에서 비슷한 효과를 본다면, transformer의 연산량을 줄일 수 있게 됩니다. 쿼리와 키의 길이를 각각 $L_Q,L_K$라고 할때 $u=c\cdot\ln L_Q$개를 선택하는 과정을 거친다면, 연산량은 $\mathcal{O} \left( L_K L_Q \right)$에서 $\mathcal{O} \left( L_K \ln L_Q \right)$로 대폭 감소하게 됩니다. 상위 $u$개가 선택된 score $\overline{M}$는 아래 식과 같으며, 그 이유를 Lemma 1.과 Appendix D로 증명합니다.
$$\overline{M}\left(\mathbf{q}_i,\mathbf{K}\right) = \max_{j} \left\{ \frac{\mathbf{q}_i\mathbf{k}_j^T}{\sqrt{d}} \right\} - \frac{1}{L_K} \sum_{j=1}^{L_K} \mathbf{q}_i\mathbf{k}_j^T / \sqrt{d}$$
저자는 attention score 연산의 개선과 별개로 Transformer 구조도 경량화를 시도합니다. 하지만 Transformer의 encoder만 경량화하며, decoder는 기존의 모듈을 사용합니다. 경량화한 구조는 아래 그림과 같습니다.

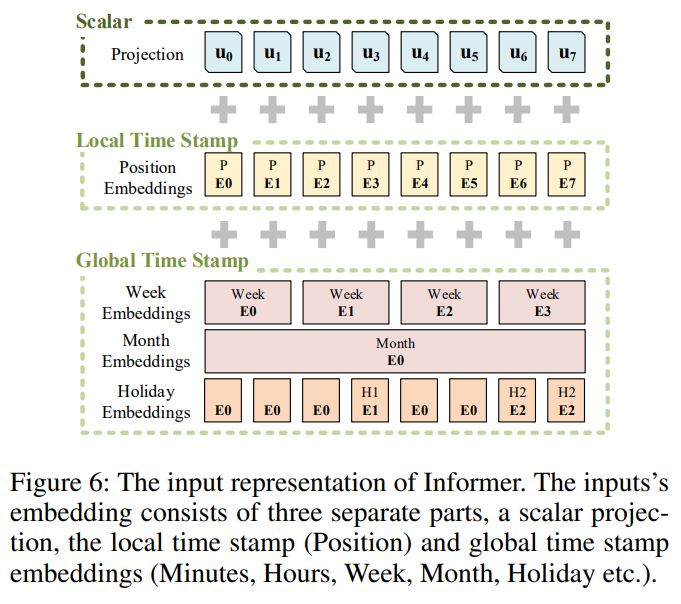
마지막으로 Transformer는 시계열 위치 정보 반영을 위해 positional embedding을 적용합니다. Informer는 단순한 위치정보 뿐만 아니라 시간의 의미를 부여하기 위해 다양한 embedding function의 합을 attention에 입력하며, embedding 적용 예제는 아래 그림입니다. 따라서, 최근 통계적 forecasting 모델들이 사용하는 단위시간당 trend를 deep learning 모델에서도 반영했다고 생각해볼 수 있습니다.
마지막으로 전체적인 흐름도는 아래 그림입니다. 눈여겨 볼 부분으로 decoder의 입력입니다. encoder의 입력 중 뒷부분을 decoder 입력의 일부인 token으로 사용합니다. 그리고 decoder로 예보할 부분들을 전부 masking 처리하여 입력하며, masking 처리된 부분을 올바르게 예측하도록 학습하는 구조를 갖습니다.

3. Experiments
Informer의 검증을 위해 Electricity Transformer Temperature (ETT) dataset을 사용합니다. 해당 데이터에 대해 LSTF를 시도한 결과 아래 그림과 같은 예측결과를 보였습니다.

저자는 단변량 시계열과 다변량 시계열 예보에 대한 성능 또한 논문의 두 표로 정리했습니다. 자세한 성능은 논문을 참고 부탁드립니다.
이와 별개로 실제 ETT dataset에 대해 Informer를 실험했을 때, 위와 같이 정교한 결과를 얻지 못했습니다. 저는 다변량으로 실험했기 때문에 정교하지 못했을 가능성이 있습니다. 하지만 제가 최근 참가하고 있는 dacon의 태양광 발전량 예보 대회에 적용했을 때, 일정 주기로 반복되는 stationary time series에 대해서는 꽤 좋은 예측 성능을 보였습니다.
Informer code는 high level API로 제공되어 어떤 점에서는 편하지만, 시간의미를 embedding하는 부분이 고정되어있기 때문에 library를 직접 수정해야할 수 있습니다. 이 점 참고하시어 저자가 제공하는 github를 사용해주시면 좋겠습니다.