2021. 12. 14. 23:36ㆍNeural Networks/Time Series
논문에 대한 오역, 의역등이 다수 포함되어 있습니다. 댓글로 많은 의견 부탁드립니다
Author: Minhao Liu, Ailing Zeng, Zhijian Xu, Qiuxia Lai, Qiang Xu
SCINet은 시계열 예보를 위해, Binary Tree 구조와 CNN unit를 활용한 forecasting 방법입니다.
모델의 성능은 링크와 같이 ETT (Electricity Transformer Temperature) dataset에서 매우 우수한 성능을 보여줍니다.
Official code는 pytorch로 구현되었으며, tensorflow로 구현한 코드도 있습니다.
1. Introduction

시계열 예보(Time series forecasting)를 위한 방법들은 지속적으로 연구되고 있습니다. 통계기반 시계열 예보 모델들은 AR부터 ARIMA, Prophet까지 발전해왔습니다. 또한 신경망 기반 예보 모델들도 RNN 기반이 강세였던 시간을 지나, temporal convolutional networks (TCN)이나 attention 기반 방법들도 등장하기 시작했습니다. 특히 지난 리뷰 중 하나인 Informer는 attention을 활용한 transformer의 연산량을 줄이면서, 효과적인 시계열 예보를 수행할 수 있었습니다.
Sample convolution and interaction network (SCINet)은 시계열을 위해 특별히 고안된 모델입니다. SCINet의 주요 골자는 다음과 같습니다.
- 다양한 시계열 해상도로부터 반복적으로 추출되고 교환하는 계층적 구조를 제안합니다.
- 계층적 구조를 위해 SCINet의 구성 요소이자 기본 단위인 SCI블럭을 제안합니다. SCI블럭은 입력 시계열이나 데이터를 다운샘플링하고, 특징들을 추출하는 역할을 수행합니다.
SCINet을 검증하기 위해, 저자들은 ETT dataset을 활용하여 실험했습니다. 그리고 SCINet은 Informer와 Informer를 개량한 Yformer보다 더 좋은 성능을 보였습니다. 관련한 논문들은 다른 분들이 작성해주신 좋은 리뷰들을 참고해주세요.
2. SCINet
긴 시계열 $X^*$와 고정된 $T$길이의 윈도우, 그리고 시간 스텝 $t$가 주어졌을 때, 과거 $T$부터 현재까지의 입력 시계열 $X$에 기반하여 예보한 시계열 $\hat{X}$는 다음과 같이 표현할 수 있습니다. 이 때, $\tau$는 예보할 시계열의 길이이고, 각 시점 $t$의 값인 $x_t \in \mathbb{R}^d$는 $d$차원의 실수입니다.
$$ \hat{X}_{t+1:t+\tau}={x_{t+1}, \cdots, x_{t+\tau}}$$
$$ X_{t-T+1:t}={x_{t-T+1}, \cdots, x_{t}}$$
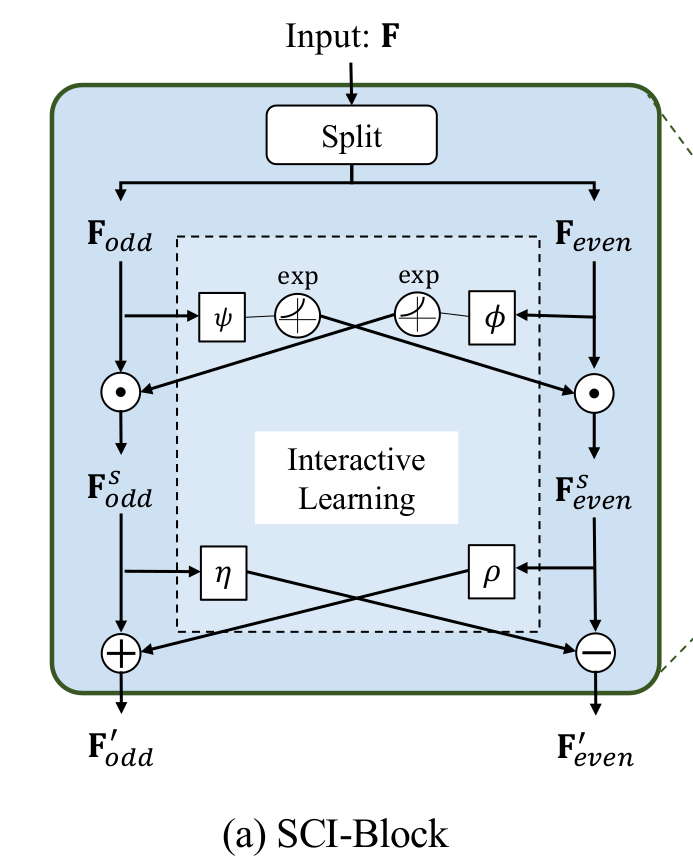
한편, SCINet의 기본 유닛인 SCI블럭은 위와 같은 구조를 갖습니다. 입력 시계열 또는 feature들을 의미하는 $F$는 $F_{odd}$와 $F_{even}$으로 나뉜 후, interactive learning을 활용한 특징 추출 과정을 거칩니다. 그림의 $\odot$은 element-wise product라고도 불리는 Hadamard product입니다. 그리고 $\psi,\phi,\eta,\rho$는 서로 다른 convolutional kernel입니다. 나뉜 $F_{odd}$와 $F_{even}$는 각기 다른 $\psi,\phi$ kernel과 exponential 함수를 순차적으로 통과합니다. 이후, $F_{odd}$는 $F_{even}$쪽으로부터 전달받는 값과 element-wise product를 계산하여 $F_{odd}^{s}$라는 feature로 변환됩니다. 반대쪽의 경우 $odd$와 $even$이 반대입니다. 다시 한번 각기 다른 $\eta,\rho$ kernel과 $\pm$ 연산자를 활용하여 SCI블럭의 feature인 $F_{odd}', F_{even}'$을 출력합니다. 위 과정을 식으로 정리하면 아래와 같습니다. 저자들은 이러한 과정을 통해 시계열 예보를 위한 long-term, short-term dependencies를 반영할 수 있다고 말합니다.
$$ F_{odd}^{s} = F_{odd} \odot \exp ( \phi ( F_{even} ) )$$
$$ F_{even}^{s} = F_{even} \odot \exp ( \psi ( F_{odd} ) ) $$
$$ F_{odd}' = F_{odd}^{s} + \rho ( F_{even}^{s} ) $$
$$ F_{even}' = F_{even}^{s} - \rho ( F_{odd}^{s} ) $$
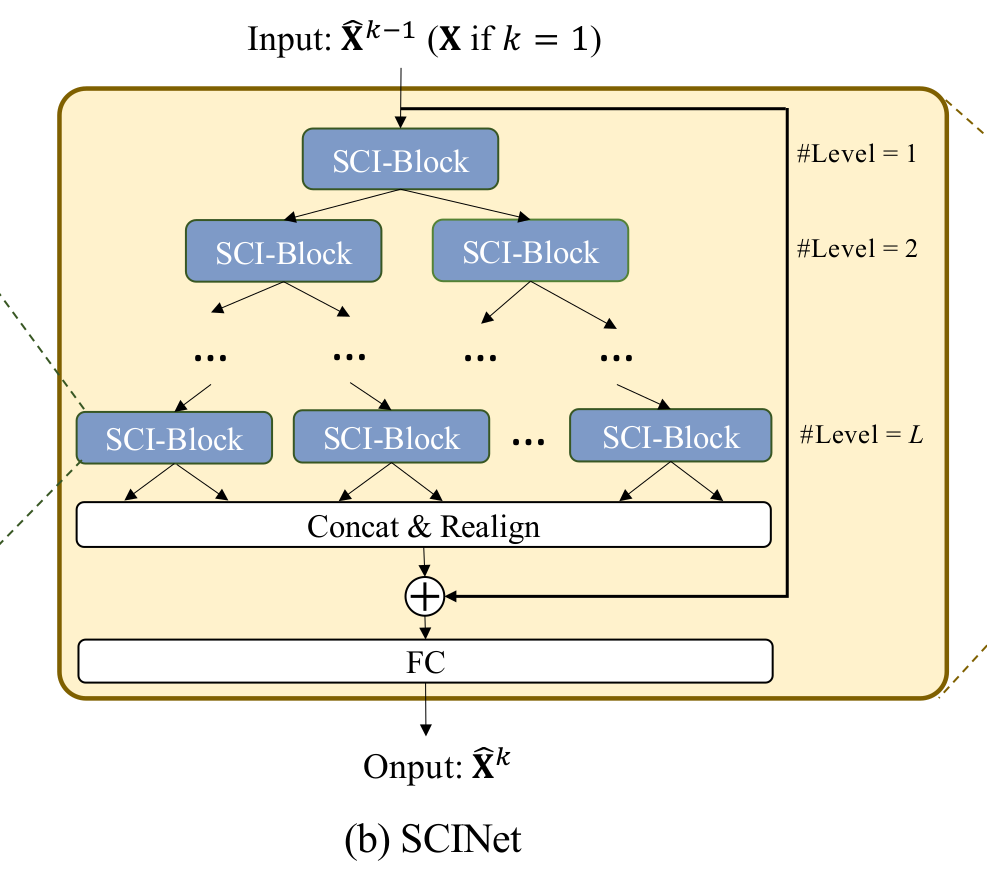
한편 나뉜 $ F_{odd}'$와 $F_{even}'$은 입력 시계열 길이 $T$의 절반이라는 점입니다. 위 그림은 SCI블럭을 활용하여 binary tree구조로 만든 SCINet입니다. 트리의 깊이 $k$가 깊어질수록 추출되는 시계열의 길이는 $\frac{T}{2^k}$를 만족합니다. 따라서, $L<\log_2T$를 만족해야 합니다. $L$ 레벨까지 추출된 feature들은 길이가 $T$인 새로운 feature들의 시계열로 병합할 수 있지만 순서가 binary tree에 따라 섞여있습니다. 추출된 feature들을 병합하고 정렬한 후, 입력 시계열의 residual connection을 더해줍니다. 마지막 linear layer는 시계열의 길이를 $T\rightarrow\tau$로 바꿔주는 역할을 수행합니다. 사용 당시 확인했을 때, Convolutional 1D layer에 kernel과 stride를 1로 사용하여 입력 시계열 길이 $T$로부터 출력 시계열 길이 $\tau$로 변환해줍니다.
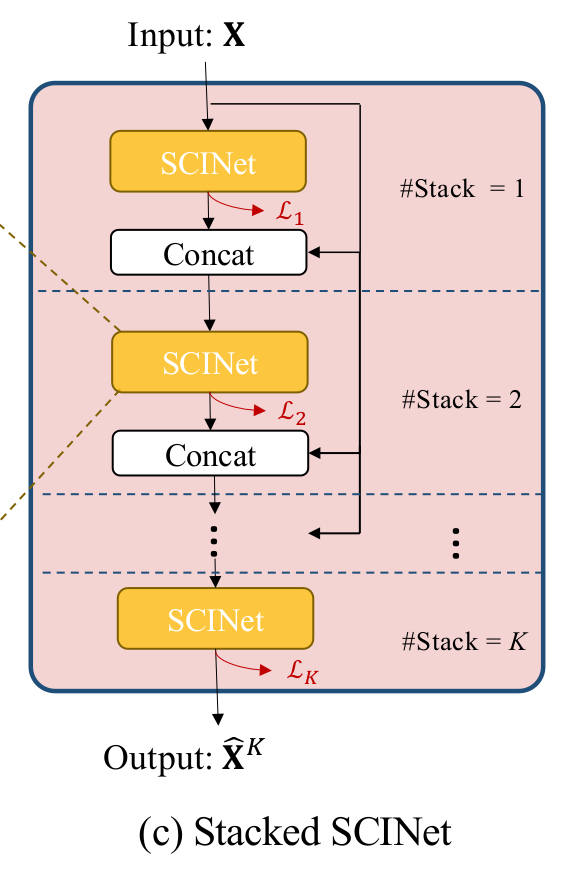
$$ \mathcal{L}_k = \frac{1}{\tau} \sum_{i=0}^{\tau} \parallel \hat{x}_i^k-x_i \parallel $$
$$ \mathcal{L} = \sum_{k=1}^{K} \mathcal{L}_k $$
마지막으로 SCINet을 $K$개만큼 stack합니다. 특별히 $K$개의 SCINet을 비슷한 관점으로 학습하기 위해, 손실함수의 식을 위와 같이 구성합니다. SCINet이 제안한 구조의 특징들은 주요 요소로 (1) 서로 다른 convolution kernel과 (2) inter-learning가 있으며, 다른 기법에서도 흔히 사용되는 방법들 중 (3) residual connection, (4) linear enhancement가 있습니다. 저자들은 제안한 4가지 요소가 유효함을 증명하기 위해, 4가지 요소를 모두 적용했을 때와, 각기 다른 한가지 요소들을 제외했을 때의 성능 차이를 비교합니다. 결과에 따르면, inter-learning의 효과가 미비한 경우도 존재하지만 ETT1h에서는 매우 좋은 효과를 거뒀습니다.
3. Result
저자는 ETT dataset을 활용하여 다양한 길이의 시계열 예보를 시도했고, SCINet이 기존의 방법들보다 더 나은 성능을 보이는 것을 경험적으로 증명합니다. 저는 시계열로부터 특징을 추출하는 encoder로써 SCINet을 활용했습니다. SCINet과 LSTM을 사용한 두 encoder를 비교했을 때 parameter도 적으면서 더 좋은 특징을 추출했기 때문에, SCINet decoder를 사용한 시계열 예측 모델이 더 좋은 손실과 metric을 보였다고 생각합니다. 자세한 결과는 리뷰 상단의 링크를 참고해주세요.